Convolution Operators

Module: pycgsp.linop.conv

Base class for graph convolution operators.

Graph convolution operator.

GraphConvolution(Graph, coefficients)

Graph convolution.
class GraphConvolution(Graph: pygsp.graphs.graph.Graph, coefficients: Union[numpy.ndarray, list, tuple])[source]

Bases: pycsou.linop.base.PolynomialLinearOperator

Graph convolution.

Convolve a signal \(\mathbf{u}\in\mathbb{C}^N\) defined on a graph with a polynomial filter \(\mathbf{D}:\mathbb{C}^N\rightarrow \mathbb{C}^N\) of the form:

\[\mathbf{D}=\sum_{k=0}^K \theta_k \mathbf{L}^k,\]

where \(\mathbf{L}:\mathbb{C}^N\rightarrow \mathbb{C}^N\) is the normalised graph Laplacian (see [FuncSphere] Section 2.3 of Chapter 6).

Examples

>>> G = RandomRegular(seed=0)
>>> G.compute_laplacian(lap_type='normalized')
>>> signal = np.random.binomial(n=1,p=0.2,size=G.N)
>>> coefficients = np.ones(shape=(3,))
>>> ConvOp = GraphConvolution(Graph=G, coefficients=coefficients)
>>> filtered = ConvOp * signal

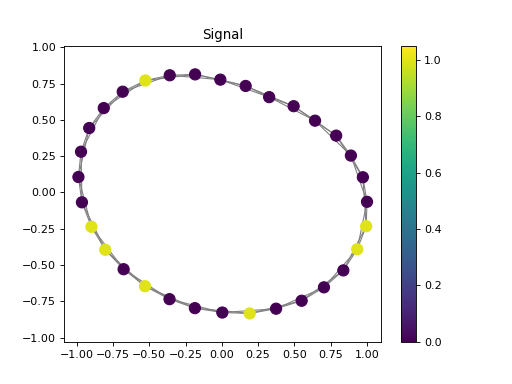
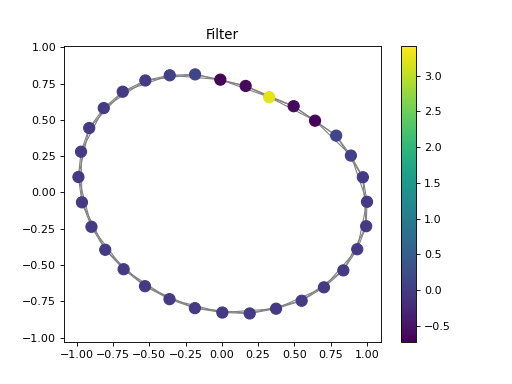
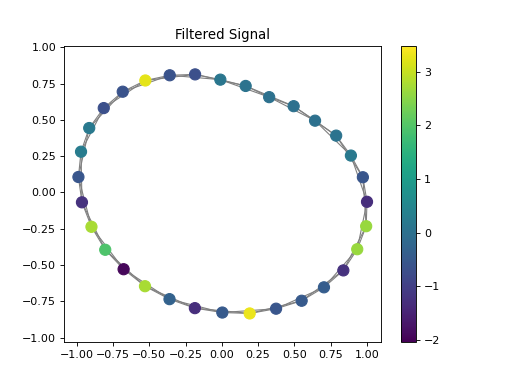
import numpy as np
from pygsp.graphs import Ring
from pycgsp.linop.conv import GraphConvolution
np.random.seed(0)
G = Ring(N=32, k=2)
G.compute_laplacian(lap_type='normalized')
G.set_coordinates(kind='spring')
signal = np.random.binomial(n=1,p=0.2,size=G.N)
coefficients = np.ones(3)
ConvOp = GraphConvolution(Graph=G, coefficients=coefficients)
e1 = np.zeros(shape=G.N)
e1[0] = 1
filter = ConvOp * e1
filtered = ConvOp * signal
plt.figure()
ax=plt.gca()
G.plot_signal(signal, ax=ax, backend='matplotlib')
plt.title('Signal')
plt.axis('equal')
plt.figure()
ax=plt.gca()
G.plot_signal(filter, ax=ax, backend='matplotlib')
plt.title('Filter')
plt.axis('equal')
plt.figure()
ax=plt.gca()
G.plot_signal(filtered, ax=ax, backend='matplotlib')
plt.title('Filtered Signal')
plt.axis('equal')

(Source code)

Notes

The GraphConvolution operator is self-adjoint and operates in a matrix-free fashion, as described in Section 4.3, Chapter 7 of [FuncSphere].

See also

GraphLaplacian

__init__(Graph: pygsp.graphs.graph.Graph, coefficients: Union[numpy.ndarray, list, tuple])[source]
Parameters
Raises