Differential Operators

Module: pycgsp.linop.diff

Base class for graph convolution operators.

Graph differential operators.

GraphLaplacian(Graph[, dtype])

Graph Laplacian.

GraphGradient(Graph[, dtype])

Graph gradient.

GeneralisedGraphLaplacian(Graph[, kind])

Generalised graph Laplacian operator.
class GraphLaplacian(Graph: pygsp.graphs.graph.Graph, dtype: type = <class 'float'>)[source]

Bases: pycsou.core.linop.LinearOperator

Graph Laplacian.

Normalised graph Laplacian for signals defined on graphs.

Examples

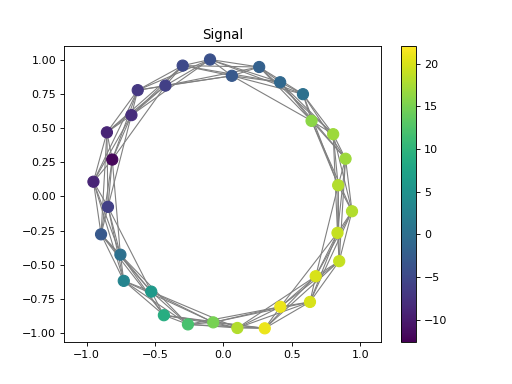
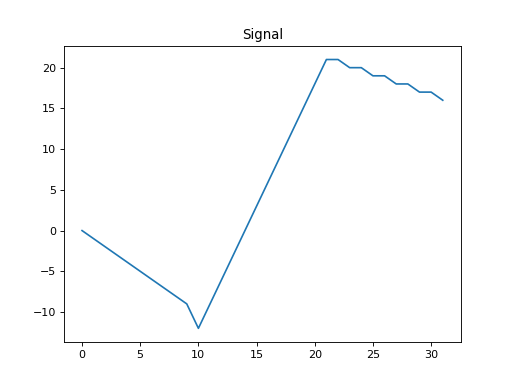
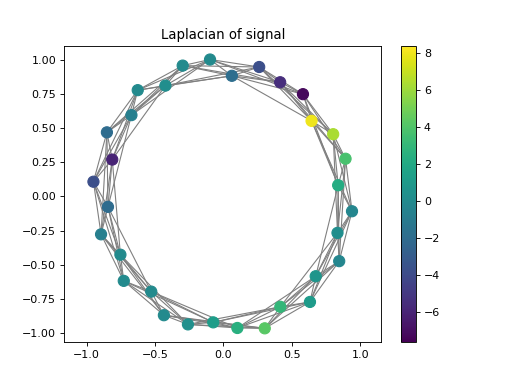
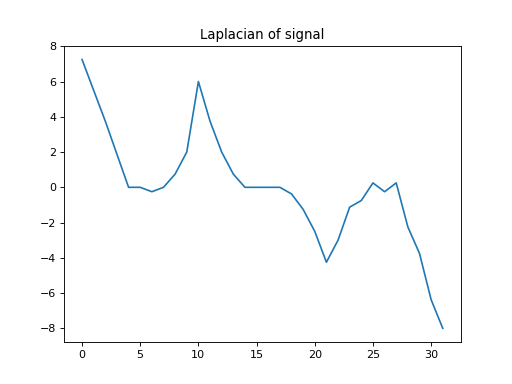
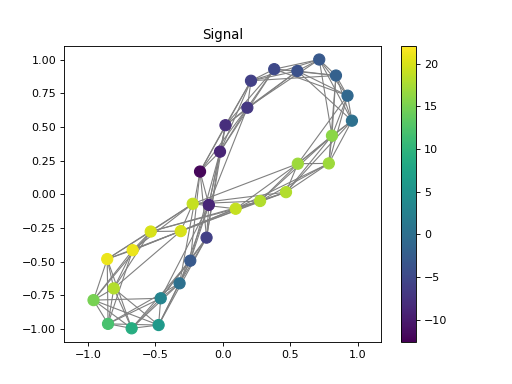
import numpy as np
from pygsp.graphs import Ring
from pycgsp.linop.diff import GraphLaplacian
np.random.seed(1)
G = Ring(N=32, k=4)
G.compute_laplacian(lap_type='normalized')
G.set_coordinates(kind='spring')
x = np.arange(G.N)
signal = np.piecewise(x, [x < G.N//3, (x >= G.N//3) * (x< 2 * G.N//3), x>=2 * G.N//3], [lambda x: -x, lambda x: 3 * x - 4 * G.N//3, lambda x: -0.5 * x + G.N])
Lap = GraphLaplacian(Graph=G)
lap_sig = Lap * signal
plt.figure()
ax=plt.gca()
G.plot_signal(signal, ax=ax, backend='matplotlib')
plt.title('Signal')
plt.axis('equal')
plt.figure()
plt.plot(signal)
plt.title('Signal')
plt.figure()
ax=plt.gca()
G.plot_signal(lap_sig, ax=ax, backend='matplotlib')
plt.title('Laplacian of signal')
plt.axis('equal')
plt.figure()
plt.plot(-lap_sig)
plt.title('Laplacian of signal')

(Source code)

Notes

For undirected graphs, the normalized graph Laplacian is defined as

\[\mathbf{L} = \mathbf{I} - \mathbf{D}^{-1/2} \mathbf{W} \mathbf{D}^{-1/2},\]

where \(\mathbf{I}\) is the identity matrix, \(\mathbf{W}\) is the weighted adjacency matrix and \(\mathbf{D}\) the weighted degree matrix.

For directed graphs, the Laplacians are built from a symmetrized version of the weighted adjacency matrix that is the average of the weighted adjacency matrix and its transpose. As the Laplacian is defined as the divergence of the gradient, it is not affected by the orientation of the edges.

For both Laplacians, the diagonal entries corresponding to disconnected nodes (i.e., nodes with degree zero) are set to zero.

The GraphLaplacian operator is self-adjoint.

See also

GraphGradient, GeneralisedGraphLaplacian() GraphConvolution

__init__(Graph: pygsp.graphs.graph.Graph, dtype: type = <class 'float'>)[source]
Parameters
Raises
adjoint(y: numpy.ndarray) → numpy.ndarray[source]

Evaluates the adjoint of the operator at a point.

Parameters

y (Union[Number, np.ndarray]) – Point at which the adjoint should be evaluated.

Returns

Evaluation of the adjoint at y.

Return type

Union[Number, np.ndarray]

class GraphGradient(Graph: pygsp.graphs.graph.Graph, dtype: type = <class 'float'>)[source]

Bases: pycsou.core.linop.LinearOperator

Graph gradient.

Gradient operator for signals defined on graphs.

Examples

>>> G = Ring(N=32, k=4)
>>> G.compute_laplacian(lap_type='normalized')
>>> G.compute_differential_operator()
>>> G.set_coordinates(kind='spring')
>>> x = np.arange(G.N)
>>> signal = np.piecewise(x, [x < G.N//3, (x >= G.N//3) * (x< 2 * G.N//3), x>=2 * G.N//3], [lambda x: -x, lambda x: 3 * x - 4 * G.N//3, lambda x: -0.5 * x + G.N])
>>> Lap = GraphLaplacian(Graph=G)
>>> Grad = GraphGradient(Graph=G)
>>> lap_sig = Lap * signal
>>> lap_sig2 = Grad.adjoint(Grad(signal))
>>> np.allclose(lap_sig, lap_sig2)
True

Notes

The adjoint of the GraphGradient operator is called the graph divergence operator.

Warning

In the newest version of PyGSP (> 0.5.1) the convention is changed: Graph.D is the divergence operator and Graph.D.transpose() the gradient (see routine Graph.compute_differential_operator). The code should be adapted when this new version is released.

See also

GraphLaplacian, GeneralisedGraphLaplacian()

__init__(Graph: pygsp.graphs.graph.Graph, dtype: type = <class 'float'>)[source]
Parameters
Raises

AttributeError – If Graph.D does not exist.

adjoint(y: numpy.ndarray) → numpy.ndarray[source]

Evaluates the adjoint of the operator at a point.

Parameters

y (Union[Number, np.ndarray]) – Point at which the adjoint should be evaluated.

Returns

Evaluation of the adjoint at y.

Return type

Union[Number, np.ndarray]

GeneralisedGraphLaplacian(Graph: pygsp.graphs.graph.Graph, kind: str = 'iterated', **kwargs)[source]

Generalised graph Laplacian operator.

Generalised Laplacian operator signals defined on graphs.

Parameters

  • Graph –

    Graph on which the signal is defined, with normalised Laplacian Graph.L precomputed (see pygsp.graphs.Graph.compute_laplacian(lap_type=’normalized’).

  • dtype (type) – Type of the entries of the graph filer.

  • kind (str) –

    Type of generalised differential operator ('iterated', 'sobolev', 'polynomial'). Depending on the cases, the GeneralisedLaplacian operator is defined as follows:

    • 'iterated': \(\mathscr{D}=\mathbf{L}^N\),

    • 'sobolev': \(\mathscr{D}=(\alpha^2 \mathrm{Id}-\mathbf{L})^N\), with \(\alpha\in\mathbb{R}\),

    • 'polynomial': \(\mathscr{D}=\sum_{n=0}^N \alpha_n \mathbf{L}^n\), with \(\{\alpha_0,\ldots,\alpha_N\} \subset\mathbb{R}\),

    where \(\mathbf{L}\) is the GraphLaplacian operator.

  • kwargs (Any) –

    Additional arguments depending on the value of kind:

    • 'iterated': kwargs={order: int} where order defines the exponent \(N\).

    • 'sobolev': kwargs={order: int, constant: float} where order defines the exponent \(N\) and constant the scalar \(\alpha\in\mathbb{R}\).

    • 'polynomial': kwargs={coeffs: Union[np.ndarray, list, tuple]} where coeffs is an array containing the coefficients \(\{\alpha_0,\ldots,\alpha_N\} \subset\mathbb{R}\).

Raises

Examples

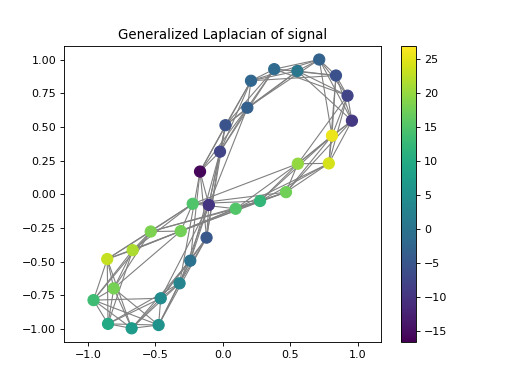
import numpy as np
from pygsp.graphs import Ring
from pycgsp.linop.diff import GeneralisedGraphLaplacian
np.random.seed(1)
G = Ring(N=32, k=4)
G.compute_laplacian(lap_type='normalized')
G.set_coordinates(kind='spring')
x = np.arange(G.N)
signal = np.piecewise(x, [x < G.N//3, (x >= G.N//3) * (x< 2 * G.N//3), x>=2 * G.N//3], [lambda x: -x, lambda x: 3 * x - 4 * G.N//3, lambda x: -0.5 * x + G.N])
Dop = GeneralisedGraphLaplacian(Graph=G, kind='polynomial', coeffs=[1,-1,2])
gen_lap = Dop * signal
plt.figure()
ax=plt.gca()
G.plot_signal(signal, ax=ax, backend='matplotlib')
plt.title('Signal')
plt.axis('equal')
plt.figure()
ax=plt.gca()
G.plot_signal(gen_lap, ax=ax, backend='matplotlib')
plt.title('Generalized Laplacian of signal')
plt.axis('equal')

(Source code)

Notes

The GeneralisedGraphLaplacian operator is self-adjoint.

See also

GraphLaplacian