Proximal Algorithms

Module: pycsou.opt.proxalgs

Proximal algorithms.

This module provides various proximal algorithms for convex optimisation.

PrimalDualSplitting(dim[, F, G, H, K, tau, …])

Primal dual splitting algorithm.

PDS

alias of pycsou.opt.proxalgs.PrimalDualSplitting

AcceleratedProximalGradientDescent(dim[, F, …])

Accelerated proximal gradient descent.

APGD

alias of pycsou.opt.proxalgs.AcceleratedProximalGradientDescent

ChambollePockSplitting(dim[, G, H, K, tau, …])

Chambolle and Pock primal-dual splitting method.

CPS

alias of pycsou.opt.proxalgs.ChambollePockSplitting

DouglasRachfordSplitting(dim[, G, H, tau, …])

Douglas Rachford splitting algorithm.

DRS

alias of pycsou.opt.proxalgs.DouglasRachfordSplitting

ForwardBackwardSplitting(dim[, F, G, tau, …])

Forward-backward splitting algorithm.

FBS

alias of pycsou.opt.proxalgs.ForwardBackwardSplitting
class PrimalDualSplitting(dim: int, F: Optional[pycsou.core.map.DifferentiableMap] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, K: Optional[pycsou.core.linop.LinearOperator] = None, tau: Optional[float] = None, sigma: Optional[float] = None, rho: Optional[float] = None, beta: Optional[float] = None, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]

Bases: pycsou.core.solver.GenericIterativeAlgorithm

Primal dual splitting algorithm.

This class is also accessible via the alias PDS().

Notes

The Primal Dual Splitting (PDS) method is described in [PDS] (this particular implementation is based on the pseudo-code Algorithm 7.1 provided in [FuncSphere] Chapter 7, Section1). It can be used to solve problems of the form:

\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{K} \mathbf{x}).}\]

where:

  • \(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).

  • \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are two proper, lower semicontinuous and convex functions with simple proximal operators.

  • \(\mathbf{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a linear operator, with operator norm:

    \[\Vert{\mathbf{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathbf{K}\mathbf{x}\Vert_2.\]

  • The problem is feasible –i.e. there exists at least one solution.

Remark 1:

The algorithm is still valid if one or more of the terms \(\mathcal{F}\), \(\mathcal{G}\) or \(\mathcal{H}\) is zero.

Remark 2:

Assume that the following holds:

  • \(\beta>0\) and:

    • \(\frac{1}{\tau}-\sigma\Vert\mathbf{K}\Vert_{2}^2\geq \frac{\beta}{2}\),

    • \(\rho \in ]0,\delta[\), where \(\delta:=2-\frac{\beta}{2}\left(\frac{1}{\tau}-\sigma\Vert\mathbf{K}\Vert_{2}^2\right)^{-1}\in[1,2[.\)

  • or \(\beta=0\) and:

    • \(\tau\sigma\Vert\mathbf{K}\Vert_{2}^2\leq 1\)

    • \(\rho \in [\epsilon,2-\epsilon]\), for some \(\epsilon>0.\)

Then, there exists a pair \((\mathbf{x}^\star,\mathbf{z}^\star)\in\mathbb{R}^N\times \mathbb{R}^M\)} solution s.t. the primal and dual sequences of estimates \((\mathbf{x}_n)_{n\in\mathbb{N}}\) and \((\mathbf{z}_n)_{n\in\mathbb{N}}\) converge towards \(\mathbf{x}^\star\) and \(\mathbf{z}^\star\) respectively, i.e.

\[\lim_{n\rightarrow +\infty}\Vert\mathbf{x}^\star-\mathbf{x}_n\Vert_2=0, \quad \text{and} \quad \lim_{n\rightarrow +\infty}\Vert\mathbf{z}^\star-\mathbf{z}_n\Vert_2=0.\]

Default values of the hyperparameters provided here always ensure convergence of the algorithm.

Examples

Consider the following optimisation problem:

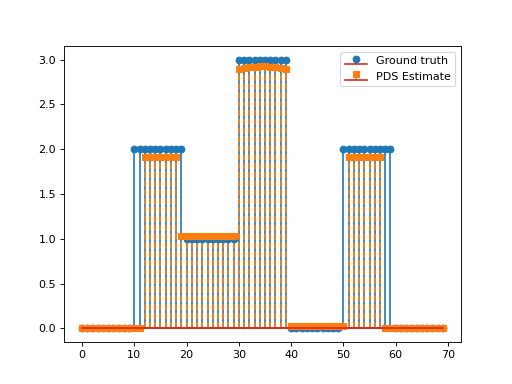
\[\min_{\mathbf{x}\in\mathbb{R}_+^N}\frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\quad+\quad\lambda_1 \|\mathbf{D}\mathbf{x}\|_1\quad+\quad\lambda_2 \|\mathbf{x}\|_1,\]

with \(\mathbf{D}\in\mathbb{R}^{N\times N}\) the discrete derivative operator and \(\mathbf{G}\in\mathbb{R}^{L\times N}, \, \mathbf{y}\in\mathbb{R}^L, \lambda_1,\lambda_2>0.\) This problem can be solved via PDS with \(\mathcal{F}(\mathbf{x})= \frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\), \(\mathcal{G}(\mathbf{x})=\lambda_2\|\mathbf{x}\|_1,\) \(\mathcal{H}(\mathbf{x})=\lambda \|\mathbf{x}\|_1\) and \(\mathbf{K}=\mathbf{D}\).

import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.diff import FirstDerivative
from pycsou.func.loss import SquaredL2Loss
from pycsou.func.penalty import L1Norm, NonNegativeOrthant
from pycsou.linop.sampling import DownSampling
from pycsou.opt.proxalgs import PrimalDualSplitting

x = np.repeat([0, 2, 1, 3, 0, 2, 0], 10)
D = FirstDerivative(size=x.size, kind='forward')
D.compute_lipschitz_cst(tol=1e-3)
rng = np.random.default_rng(0)
G = DownSampling(size=x.size, downsampling_factor=3)
G.compute_lipschitz_cst()
y = G(x)
l22_loss = (1 / 2) * SquaredL2Loss(dim=G.shape[0], data=y)
F = l22_loss * G
lambda_ = 0.1
H = lambda_ * L1Norm(dim=D.shape[0])
G = 0.01 * L1Norm(dim=G.shape[1])
pds = PrimalDualSplitting(dim=G.shape[1], F=F, G=G, H=H, K=D, verbose=None)
estimate, converged, diagnostics = pds.iterate()
plt.figure()
plt.stem(x, linefmt='C0-', markerfmt='C0o')
plt.stem(estimate['primal_variable'], linefmt='C1--', markerfmt='C1s')
plt.legend(['Ground truth', 'PDS Estimate'])
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-opt-proxalgs-1.png

See also

PDS, ChambollePockSplitting, DouglasRachford

__init__(dim: int, F: Optional[pycsou.core.map.DifferentiableMap] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, K: Optional[pycsou.core.linop.LinearOperator] = None, tau: Optional[float] = None, sigma: Optional[float] = None, rho: Optional[float] = None, beta: Optional[float] = None, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]
Parameters

  • dim (int) – Dimension of the objective functional’s domain.

  • F (Optional[DifferentiableMap]) – Differentiable map \(\mathcal{F}\).

  • G (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{G}\).

  • H (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{H}\).

  • K (Optional[LinearOperator]) – Linear operator \(\mathbf{K}\).

  • tau (Optional[float]) – Primal step size.

  • sigma (Optional[float]) – Dual step size.

  • rho (Optional[float]) – Momentum parameter.

  • beta (Optional[float]) – Lipschitz constant \(\beta\) of the derivative of \(\mathcal{F}\).

  • x0 (Optional[np.ndarray]) – Initial guess for the primal variable.

  • z0 (Optional[np.ndarray]) – Initial guess for the dual variable.

  • max_iter (int) – Maximal number of iterations.

  • min_iter (int) – Minimal number of iterations.

  • accuracy_threshold (float) – Accuracy threshold for stopping criterion.

  • verbose (int) – Print diagnostics every verbose iterations. If None does not print anything.

set_step_sizes() → Tuple[float, float][source]

Set the primal/dual step sizes.

Returns

Sensible primal/dual step sizes.

Return type

Tuple[float, float]

Notes

In practice, the convergence speed of the algorithm is improved by choosing \(\sigma\) and \(\tau\) as large as possible and relatively well-balanced –so that both the primal and dual variables converge at the same pace. In practice, it is hence recommended to choose perfectly balanced parameters \(\sigma=\tau\) saturating the convergence inequalities.

For \(\beta>0\) this yields:

\[\frac{1}{\tau}-\tau\Vert\mathbf{K}\Vert_{2}^2= \frac{\beta}{2} \quad\Longleftrightarrow\quad -2\tau^2\Vert\mathbf{K}\Vert_{2}^2-\beta\tau+2=0,\]

which admits one positive root

\[\tau=\sigma=\frac{1}{\Vert\mathbf{K}\Vert_{2}^2}\left(-\frac{\beta}{4}+\sqrt{\frac{\beta^2}{16}+\Vert\mathbf{K}\Vert_{2}^2}\right).\]

For \(\beta=0\), this yields

\[\tau=\sigma=\Vert\mathbf{K\Vert_{2}^{-1}.}\]
set_momentum_term() → float[source]

Sets the momentum term.

Returns

Momentum term.

Return type

float

initialize_primal_variable() → numpy.ndarray[source]

Initialize the primal variable to zero.

Returns

Zero-initialized primal variable.

Return type

np.ndarray

initialize_dual_variable() → Optional[numpy.ndarray][source]

Initialize the dual variable to zero.

Returns

Zero-initialized dual variable.

Return type

np.ndarray

update_iterand() → dict[source]

Update the iterand.

Returns

Result of the update.

Return type

Any

print_diagnostics()[source]

Print diagnostics.

stopping_metric()[source]

Stopping metric.

update_diagnostics()[source]

Update the diagnostics.

PDS

alias of pycsou.opt.proxalgs.PrimalDualSplitting

class AcceleratedProximalGradientDescent(dim: int, F: Optional[pycsou.core.map.DifferentiableMap] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: Optional[float] = None, acceleration: Optional[str] = 'CD', beta: Optional[float] = None, x0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1, d: float = 75.0)[source]

Bases: pycsou.core.solver.GenericIterativeAlgorithm

Accelerated proximal gradient descent.

This class is also accessible via the alias APGD().

Notes

The Accelerated Proximal Gradient Descent (APGD) method can be used to solve problems of the form:

\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x}).}\]

where:

  • \(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).

  • \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) is a proper, lower semicontinuous and convex function with a simple proximal operator.

  • The problem is feasible –i.e. there exists at least one solution.

Remark 1: the algorithm is still valid if one or more of the terms \(\mathcal{F}\) or \(\mathcal{G}\) is zero.

Remark 2: The convergence is guaranteed for step sizes \(\tau\leq 1/\beta\). Without acceleration, APGD can be seen as a PDS method with \(\rho=1\). The various acceleration schemes are described in [APGD]. For \(0<\tau\leq 1/\beta\) and Chambolle and Dossal’s acceleration scheme (acceleration='CD'), APGD achieves the following (optimal) convergence rates:

\[\lim\limits_{n\rightarrow \infty} n^2\left\vert \mathcal{J}(\mathbf{x}^\star)- \mathcal{J}(\mathbf{x}_n)\right\vert=0\qquad \&\qquad \lim\limits_{n\rightarrow \infty} n^2\Vert \mathbf{x}_n-\mathbf{x}_{n-1}\Vert^2_\mathcal{X}=0,\]

for some minimiser \({\mathbf{x}^\star}\in\arg\min_{\mathbf{x}\in\mathbb{R}^N} \;\left\{\mathcal{J}(\mathbf{x}):=\mathcal{F}(\mathbf{x})+\mathcal{G}(\mathbf{x})\right\}\). In other words, both the objective functional and the APGD iterates \(\{\mathbf{x}_n\}_{n\in\mathbb{N}}\) converge at a rate \(o(1/n^2)\). In comparison Beck and Teboule’s acceleration scheme (acceleration='BT') only achieves a convergence rate of \(O(1/n^2)\). Significant practical speedup can moreover be achieved for values of \(d\) in the range \([50,100]\) [APGD].

Examples

Consider the LASSO problem:

\[\min_{\mathbf{x}\in\mathbb{R}^N}\frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\quad+\quad\lambda \|\mathbf{x}\|_1,\]

with \(\mathbf{G}\in\mathbb{R}^{L\times N}, \, \mathbf{y}\in\mathbb{R}^L, \lambda>0.\) This problem can be solved via APGD with \(\mathcal{F}(\mathbf{x})= \frac{1}{2}\left\|\mathbf{y}-\mathbf{G}\mathbf{x}\right\|_2^2\) and \(\mathcal{G}(\mathbf{x})=\lambda \|\mathbf{x}\|_1\). We have:

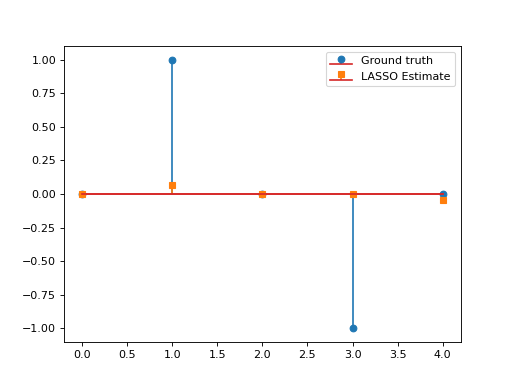
\[\mathbf{\nabla}\mathcal{F}(\mathbf{x})=\mathbf{G}^T(\mathbf{G}\mathbf{x}-\mathbf{y}), \qquad \text{prox}_{\lambda\|\cdot\|_1}(\mathbf{x})=\text{soft}_\lambda(\mathbf{x}).\]

This yields the so-called Fast Iterative Soft Thresholding Algorithm (FISTA), whose convergence is guaranteed for \(d>2\) and \(0<\tau\leq \beta^{-1}=\|\mathbf{G}\|_2^{-2}\).

import numpy as np
import matplotlib.pyplot as plt
from pycsou.func.loss import SquaredL2Loss
from pycsou.func.penalty import L1Norm
from pycsou.linop.base import DenseLinearOperator
from pycsou.opt.proxalgs import APGD

rng = np.random.default_rng(0)
G = DenseLinearOperator(rng.standard_normal(15).reshape(3,5))
G.compute_lipschitz_cst()
x = np.zeros(G.shape[1])
x[1] = 1
x[-2] = -1
y = G(x)
l22_loss = (1/2) * SquaredL2Loss(dim=G.shape[0], data=y)
F = l22_loss * G
lambda_ = 0.9 * np.max(np.abs(F.gradient(0 * x)))
G = lambda_ * L1Norm(dim=G.shape[1])
apgd = APGD(dim=G.shape[1], F=F, G=G, acceleration='CD', verbose=None)
estimate, converged, diagnostics = apgd.iterate()
plt.figure()
plt.stem(x, linefmt='C0-', markerfmt='C0o')
plt.stem(estimate['iterand'], linefmt='C1--', markerfmt='C1s')
plt.legend(['Ground truth', 'LASSO Estimate'])
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-opt-proxalgs-2.png

See also

APGD

__init__(dim: int, F: Optional[pycsou.core.map.DifferentiableMap] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: Optional[float] = None, acceleration: Optional[str] = 'CD', beta: Optional[float] = None, x0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1, d: float = 75.0)[source]
Parameters

  • dim (int) – Dimension of the objective functional’s domain.

  • F (Optional[DifferentiableMap]) – Differentiable map \(\mathcal{F}\).

  • G (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{G}\).

  • tau (Optional[float]) – Primal step size.

  • acceleration (Optional[str] [None, 'BT', 'CD']) – Which acceleration scheme should be used (None for no acceleration).

  • beta (Optional[float]) – Lipschitz constant \(\beta\) of the derivative of \(\mathcal{F}\).

  • x0 (Optional[np.ndarray]) – Initial guess for the primal variable.

  • max_iter (int) – Maximal number of iterations.

  • min_iter (int) – Minimal number of iterations.

  • accuracy_threshold (float) – Accuracy threshold for stopping criterion.

  • verbose (int) – Print diagnostics every verbose iterations. If None does not print anything.

  • d (float) – Parameter \(d\) for Chambolle and Dossal’s acceleration scheme (acceleration='CD').

set_step_size() → float[source]

Set the step size to its largest admissible value \(1/\beta\).

Returns

Largest admissible step size.

Return type

Tuple[float, float]

initialize_iterate() → numpy.ndarray[source]

Initialize the iterand to zero.

Returns

Zero-initialized iterand.

Return type

np.ndarray

update_iterand() → Any[source]

Update the iterand.

Returns

Result of the update.

Return type

Any

print_diagnostics()[source]

Print diagnostics.

stopping_metric()[source]

Stopping metric.

update_diagnostics()[source]

Update the diagnostics.

APGD

alias of pycsou.opt.proxalgs.AcceleratedProximalGradientDescent

class ChambollePockSplitting(dim: int, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, K: Optional[pycsou.core.linop.LinearOperator] = None, tau: Optional[float] = None, sigma: Optional[float] = None, rho: Optional[float] = 1, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]

Bases: pycsou.opt.proxalgs.PrimalDualSplitting

Chambolle and Pock primal-dual splitting method.

This class is also accessible via the alias CPS().

Notes

The Chambolle and Pock primal-dual splitting (CPS) method can be used to solve problems of the form:

\[{\min_{\mathbf{x}\in\mathbb{R}^N} \mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{K} \mathbf{x}).}\]

where:

  • \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are two proper, lower semicontinuous and convex functions with simple proximal operators.

  • \(\mathbf{K}:\mathbb{R}^N\rightarrow \mathbb{R}^M\) is a linear operator, with operator norm:

    \[\Vert{\mathbf{K}}\Vert_2=\sup_{\mathbf{x}\in\mathbb{R}^N,\Vert\mathbf{x}\Vert_2=1} \Vert\mathbf{K}\mathbf{x}\Vert_2.\]

  • The problem is feasible –i.e. there exists at least one solution.

Remark 1:

The algorithm is still valid if one of the terms \(\mathcal{G}\) or \(\mathcal{H}\) is zero.

Remark 2:

Assume that the following holds:

  • \(\tau\sigma\Vert\mathbf{K}\Vert_{2}^2\leq 1\)

  • \(\rho \in [\epsilon,2-\epsilon]\), for some \(\epsilon>0.\)

Then, there exists a pair \((\mathbf{x}^\star,\mathbf{z}^\star)\in\mathbb{R}^N\times \mathbb{R}^M\)} solution s.t. the primal and dual sequences of estimates \((\mathbf{x}_n)_{n\in\mathbb{N}}\) and \((\mathbf{z}_n)_{n\in\mathbb{N}}\) converge towards \(\mathbf{x}^\star\) and \(\mathbf{z}^\star\) respectively, i.e.

\[\lim_{n\rightarrow +\infty}\Vert\mathbf{x}^\star-\mathbf{x}_n\Vert_2=0, \quad \text{and} \quad \lim_{n\rightarrow +\infty}\Vert\mathbf{z}^\star-\mathbf{z}_n\Vert_2=0.\]

Default values of the hyperparameters provided here always ensure convergence of the algorithm.

See also

CPS, PrimalDualSplitting, DouglasRachfordSplitting

__init__(dim: int, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, K: Optional[pycsou.core.linop.LinearOperator] = None, tau: Optional[float] = None, sigma: Optional[float] = None, rho: Optional[float] = 1, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]
Parameters

  • dim (int) – Dimension of the objective functional’s domain.

  • G (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{G}\).

  • H (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{H}\).

  • K (Optional[LinearOperator]) – Linear operator \(\mathbf{K}\).

  • tau (Optional[float]) – Primal step size.

  • sigma (Optional[float]) – Dual step size.

  • rho (Optional[float]) – Momentum parameter.

  • x0 (Optional[np.ndarray]) – Initial guess for the primal variable.

  • z0 (Optional[np.ndarray]) – Initial guess for the dual variable.

  • max_iter (int) – Maximal number of iterations.

  • min_iter (int) – Minimal number of iterations.

  • accuracy_threshold (float) – Accuracy threshold for stopping criterion.

  • verbose (int) – Print diagnostics every verbose iterations. If None does not print anything.

CPS

alias of pycsou.opt.proxalgs.ChambollePockSplitting

class DouglasRachfordSplitting(dim: int, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: float = 1.0, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]

Bases: pycsou.opt.proxalgs.PrimalDualSplitting

Douglas Rachford splitting algorithm.

This class is also accessible via the alias DRS().

Notes

The Douglas Rachford Splitting (DRS) can be used to solve problems of the form:

\[{\min_{\mathbf{x}\in\mathbb{R}^N} \mathcal{G}(\mathbf{x})\;\;+\;\;\mathcal{H}(\mathbf{x}).}\]

where:

  • \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) and \(\mathcal{H}:\mathbb{R}^M\rightarrow \mathbb{R}\cup\{+\infty\}\) are two proper, lower semicontinuous and convex functions with simple proximal operators.

  • The problem is feasible –i.e. there exists at least one solution.

Remark 1:

The algorithm is still valid if one of the terms \(\mathcal{G}\) or \(\mathcal{H}\) is zero.

Default values of the hyperparameters provided here always ensure convergence of the algorithm.

See also

DRS, PrimalDualSplitting, ChambollePockSplitting

__init__(dim: int, G: Optional[pycsou.core.functional.ProximableFunctional] = None, H: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: float = 1.0, x0: Optional[numpy.ndarray] = None, z0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]
Parameters

  • dim (int) – Dimension of the objective functional’s domain.

  • G (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{G}\).

  • H (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{H}\).

  • tau (Optional[float]) – Primal step size.

  • x0 (Optional[np.ndarray]) – Initial guess for the primal variable.

  • z0 (Optional[np.ndarray]) – Initial guess for the dual variable.

  • max_iter (int) – Maximal number of iterations.

  • min_iter (int) – Minimal number of iterations.

  • accuracy_threshold (float) – Accuracy threshold for stopping criterion.

  • verbose (int) – Print diagnostics every verbose iterations. If None does not print anything.

DRS

alias of pycsou.opt.proxalgs.DouglasRachfordSplitting

class ForwardBackwardSplitting(dim: int, F: Optional[pycsou.core.functional.DifferentiableFunctional] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: Optional[float] = None, rho: Optional[float] = 1, x0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]

Bases: pycsou.opt.proxalgs.PrimalDualSplitting

Forward-backward splitting algorithm.

This class is also accessible via the alias FBS().

Notes

The Forward-backward splitting (FBS) method can be used to solve problems of the form:

\[{\min_{\mathbf{x}\in\mathbb{R}^N} \;\mathcal{F}(\mathbf{x})\;\;+\;\;\mathcal{G}(\mathbf{x}).}\]

where:

  • \(\mathcal{F}:\mathbb{R}^N\rightarrow \mathbb{R}\) is convex and differentiable, with \(\beta\)-Lipschitz continuous gradient, for some \(\beta\in[0,+\infty[\).

  • \(\mathcal{G}:\mathbb{R}^N\rightarrow \mathbb{R}\cup\{+\infty\}\) is proper, lower semicontinuous and convex function with simple proximal operator.

  • The problem is feasible –i.e. there exists at least one solution.

Remark 1:

The algorithm is still valid if one of the terms \(\mathcal{F}\) or \(\mathcal{G}\) is zero.

Remark 2:

Assume that the following holds:

  • \(\frac{1}{\tau}\geq \frac{\beta}{2}\),

  • \(\rho \in ]0,\delta[\), where \(\delta:=2-\frac{\beta}{2}\tau\in[1,2[.\)

Then, there exists a pair \((\mathbf{x}^\star,\mathbf{z}^\star)\in\mathbb{R}^N\times \mathbb{R}^M\)} solution s.t. the primal and dual sequences of estimates \((\mathbf{x}_n)_{n\in\mathbb{N}}\) and \((\mathbf{z}_n)_{n\in\mathbb{N}}\) converge towards \(\mathbf{x}^\star\) and \(\mathbf{z}^\star\) respectively, i.e.

\[\lim_{n\rightarrow +\infty}\Vert\mathbf{x}^\star-\mathbf{x}_n\Vert_2=0, \quad \text{and} \quad \lim_{n\rightarrow +\infty}\Vert\mathbf{z}^\star-\mathbf{z}_n\Vert_2=0.\]

Default values of the hyperparameters provided here always ensure convergence of the algorithm.

See also

FBS, AcceleratedProximalGradientDescent

__init__(dim: int, F: Optional[pycsou.core.functional.DifferentiableFunctional] = None, G: Optional[pycsou.core.functional.ProximableFunctional] = None, tau: Optional[float] = None, rho: Optional[float] = 1, x0: Optional[numpy.ndarray] = None, max_iter: int = 500, min_iter: int = 10, accuracy_threshold: float = 0.001, verbose: Optional[int] = 1)[source]
Parameters

  • dim (int) – Dimension of the objective functional’s domain.

  • F (Optional[DifferentiableMap]) – Differentiable map \(\mathcal{F}\).

  • G (Optional[ProximableFunctional]) – Proximable functional \(\mathcal{G}\).

  • tau (Optional[float]) – Primal step size.

  • rho (Optional[float]) – Momentum parameter.

  • beta (Optional[float]) – Lipschitz constant \(\beta\) of the derivative of \(\mathcal{F}\).

  • x0 (Optional[np.ndarray]) – Initial guess for the primal variable.

  • max_iter (int) – Maximal number of iterations.

  • min_iter (int) – Minimal number of iterations.

  • accuracy_threshold (float) – Accuracy threshold for stopping criterion.

  • verbose (int) – Print diagnostics every verbose iterations. If None does not print anything.

FBS

alias of pycsou.opt.proxalgs.ForwardBackwardSplitting