Convolution Operators

Module: pycsou.linop.conv

Convolution and smoothing operators for 1D, 2D and graph signals.

Many of the linear operator provided in this module are derived from linear operators from PyLops.

1D Operators

Convolve1D(size, filter[, reshape_dims, …])

1D convolution operator.

Convolve2D(size, filter, shape[, dtype, method])

2D convolution operator.

MovingAverage1D(window_size, shape[, axis, …])

1D moving average.

2D Operators

Convolve2D(size, filter, shape[, dtype, method])

2D convolution operator.

MovingAverage2D(window_shape, shape[, dtype])

2D moving average.
Convolve1D(size: int, filter: numpy.ndarray, reshape_dims: Optional[tuple] = None, axis: int = 0, dtype: type = 'float64', method: Optional[str] = None) → pycsou.linop.base.PyLopLinearOperator[source]

1D convolution operator.

This docstring was adapted from ``pylops.signalprocessing.Convolve1D``.

Convolve a multi-dimensional array along a specific axis with a one-dimensional compact filter.

Parameters

  • size (int) – Size of the input array.

  • filter (np.ndarray) – 1d compact filter. The latter should be real-valued and centered around its mid-size index.

  • reshape_dims (Optional[tuple]) – Shape of the array to which the convolution should be applied.

  • axis (int) – Axis along which to apply convolution.

  • dtype (str) – Type of elements of the input array.

  • method (Optional[str]) – Method used to calculate the convolution (direct, fft, or overlapadd). Note that only direct and fft are allowed when dims=None, whilst fft and overlapadd are allowed when dims is provided.

Returns

Convolution operator.

Return type

pycsou.linop.base.PyLopLinearOperator

Raises

NotImplementedError – If method provided is not allowed.

Examples

>>> sig = np.repeat([0., 1., 0.], 10)
>>> filter = signal.hann(5); filter[filter.size//2:] = 0
>>> ConvOp = Convolve1D(size=sig.size, filter=filter)
>>> filtered = ConvOp * sig
>>> filtered_scipy = signal.convolve(sig, filter, mode='same', method='direct')
>>> np.allclose(filtered, filtered_scipy)
True

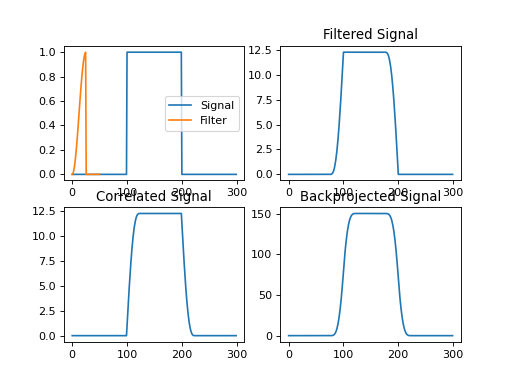
import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.conv import Convolve1D
from scipy import signal
sig = np.repeat([0., 1., 0.], 100)
filter = signal.hann(50); filter[filter.size//2:] = 0
ConvOp = Convolve1D(size=sig.size, filter=filter)
filtered = ConvOp * sig
correlated = ConvOp.H * sig
backprojected = ConvOp.DomainGram * sig
plt.figure()
plt.subplot(2,2,1)
plt.plot(sig); plt.plot(np.linspace(0, 50, filter.size), filter); plt.legend(['Signal', 'Filter'])
plt.subplot(2,2,2)
plt.plot(filtered); plt.title('Filtered Signal')
plt.subplot(2,2,3)
plt.plot(correlated); plt.title('Correlated Signal')
plt.subplot(2,2,4)
plt.plot(backprojected); plt.title('Backprojected Signal')
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-linop-conv-1.png 
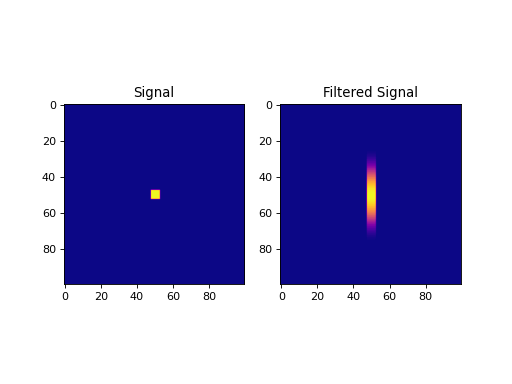
import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.conv import Convolve1D
from scipy import signal
sig = np.zeros(shape=(100,100))
sig[sig.shape[0] // 2 - 2:sig.shape[0] // 2 + 3, sig.shape[1] // 2 - 2:sig.shape[1] // 2 + 3] = 1
filter = signal.hann(50)
ConvOp = Convolve1D(size=sig.size, filter=filter, reshape_dims=sig.shape, axis=0)
filtered = (ConvOp * sig.reshape(-1)).reshape(sig.shape)
plt.figure()
plt.subplot(1,2,1)
plt.imshow(sig, cmap='plasma'); plt.title('Signal')
plt.subplot(1,2,2)
plt.imshow(filtered, cmap='plasma'); plt.title('Filtered Signal')
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-linop-conv-2.png

Notes

The Convolve1D operator applies convolution between the input signal \(x(t)\) and a compact filter kernel \(h(t)\) in forward model:

\[y(t) = \int_{-\infty}^{\infty} h(t-\tau) x(\tau) d\tau\]

This operation can be discretized as follows

\[y[n] = \sum_{m\in\mathbb{Z}} h[n-m] x[m], \, n\in\mathbb{Z},\]

as well as performed in the frequency domain:

\[Y(f) = \mathscr{F} (h(t)) \times \mathscr{F} (x(t)),\; f\in\mathbb{R}.\]

Convolve1D operator uses scipy.signal.convolve() that automatically chooses the best method for computing the convolution for one dimensional inputs. The FFT implementation scipy.signal.fftconvolve() is however enforced for signals in 2 or more dimensions as this routine efficiently operates on multi-dimensional arrays. The method overlapadd uses scipy.signal.oaconvolve().

As the adjoint of convolution is correlation, Convolve1D operator applies correlation in the adjoint mode.

In time domain:

\[x(t) = \int_{-\infty}^{\infty} h(t+\tau) x(\tau) d\tau\]

or in frequency domain:

\[y(t) = \mathscr{F}^{-1} (H(f)^\ast \times X(f)).\]

See also

Convolve2D()

Convolve2D(size: int, filter: numpy.ndarray, shape: tuple, dtype: type = 'float64', method: str = 'fft') → pycsou.linop.base.PyLopLinearOperator[source]

2D convolution operator.

This docstring was adapted from ``pylops.signalprocessing.Convolve2D``.

Convolve a two-dimensional array with a two-dimensional compact filter.

Parameters

  • size (int) – Size of the input array.

  • filter (np.ndarray) – 2d compact filter. The latter should be real-valued and centered around its central indices.

  • shape (tuple) – Shape of the array to which the convolution should be applied.

  • dtype (str) – Type of elements of the input array.

  • method (str) – Method used to calculate the convolution (direct or fft).

Returns

Convolution operator.

Return type

pycsou.linop.base.PyLopLinearOperator

Raises

ValueError – If filter is not a 2D array.

Examples

>>> sig = np.zeros(shape=(100,100))
>>> sig[sig.shape[0] // 2 - 2:sig.shape[0] // 2 + 3, sig.shape[1] // 2 - 2:sig.shape[1] // 2 + 3] = 1
>>> filter = signal.hann(25); filter[filter.size//2:] = 0
>>> filter = filter[None,:] * filter[:,None]
>>> ConvOp = Convolve2D(size=sig.size, filter=filter, shape=sig.shape)
>>> filtered = (ConvOp * sig.ravel()).reshape(sig.shape)
>>> filtered_scipy = signal.convolve(sig, filter, mode='same', method='fft')
>>> np.allclose(filtered, filtered_scipy)
True

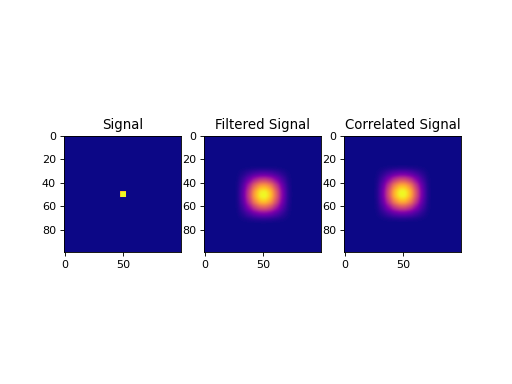
import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.conv import Convolve2D
from scipy import signal
sig = np.zeros(shape=(100,100))
sig[sig.shape[0] // 2 - 2:sig.shape[0] // 2 + 3, sig.shape[1] // 2 - 2:sig.shape[1] // 2 + 3] = 1
filter = signal.hann(50)
filter = filter[None,:] * filter[:,None]
ConvOp = Convolve2D(size=sig.size, filter=filter, shape=sig.shape)
filtered = (ConvOp * sig.ravel()).reshape(sig.shape)
correlated = (ConvOp.H * sig.ravel()).reshape(sig.shape)
plt.figure()
plt.subplot(1,3,1)
plt.imshow(sig, cmap='plasma'); plt.title('Signal')
plt.subplot(1,3,2)
plt.imshow(filtered, cmap='plasma'); plt.title('Filtered Signal')
plt.subplot(1,3,3)
plt.imshow(correlated, cmap='plasma'); plt.title('Correlated Signal')
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-linop-conv-3.png

Notes

The Convolve2D operator applies two-dimensional convolution between the input signal \(d(t,x)\) and a compact filter kernel \(h(t,x)\) in forward model:

\[y(t,x) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} h(t-\tau,x-\chi) d(\tau,\chi) d\tau d\chi\]

This operation can be discretized as follows

\[y[i,n] = \sum_{j=-\infty}^{\infty} \sum_{m=-\infty}^{\infty} h[i-j,n-m] d[j,m]\]

as well as performed in the frequency domain:

\[Y(f, k_x) = \mathscr{F} (h(t,x)) \times \mathscr{F} (d(t,x)).\]

Convolve2D operator uses scipy.signal.convolve() that automatically chooses the best domain for the operation to be carried out.

As the adjoint of convolution is correlation, Convolve2D operator applies correlation in the adjoint mode.

In time domain:

\[y(t,x) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} h(t+\tau,x+\chi) d(\tau,\chi) d\tau d\chi\]

or in frequency domain:

\[y(t, x) = \mathscr{F}^{-1} (H(f, k_x)^\ast \times X(f, k_x)).\]

See also

Convolve1D()

MovingAverage1D(window_size: int, shape: tuple, axis: int = 0, dtype='float64')[source]

1D moving average.

Apply moving average to a multi-dimensional array along a specific axis.

Parameters

  • window_size (int) – Size of the window for moving average (must be odd).

  • shape (tuple) – Shape of the input array.

  • axis (int) – Axis along which moving average is applied.

  • dtype (str) – Type of elements in input array.

Returns

1D moving average operator.

Return type

pycsou.linop.base.PyLopLinearOperator

Examples

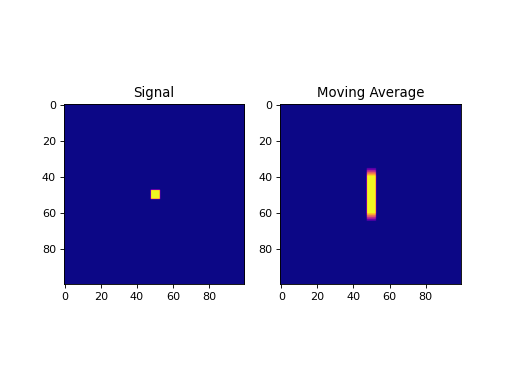
import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.conv import MovingAverage1D
from scipy import signal
sig = np.zeros(shape=(100,100))
sig[sig.shape[0] // 2 - 2:sig.shape[0] // 2 + 3, sig.shape[1] // 2 - 2:sig.shape[1] // 2 + 3] = 1
MAOp = MovingAverage1D(window_size=25, shape=sig.shape, axis=0)
moving_average = (MAOp * sig.ravel()).reshape(sig.shape)
plt.figure()
plt.subplot(1,2,1)
plt.imshow(sig, cmap='plasma'); plt.title('Signal')
plt.subplot(1,2,2)
plt.imshow(moving_average, cmap='plasma'); plt.title('Moving Average')
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-linop-conv-4.png

Notes

The MovingAverage1D operator is a special type of convolution operator that convolves along a specific axis an array with a constant filter of size \(n_{smooth}\):

\[\mathbf{h} = [ 1/n_{smooth}, 1/n_{smooth}, ..., 1/n_{smooth} ]\]

For example, for a 3D array \(x\), MovingAverage1D applied to the first axis yields:

\[y[i,j,k] = 1/n_{smooth} \sum_{l=-(n_{smooth}-1)/2}^{(n_{smooth}-1)/2} x[l,j,k].\]

Note that since the filter is symmetrical, the MovingAverage1D operator is self-adjoint.

MovingAverage2D(window_shape: Union[tuple, list], shape: tuple, dtype='float64')[source]

2D moving average.

Apply moving average to a 2D array.

Parameters

  • window_size (Union[tuple, list]) – Shape of the window for moving average (sizes in each dimension must be odd).

  • shape (tuple) – Shape of the input array.

  • dtype (str) – Type of elements in input array.

Returns

2D moving average operator.

Return type

pycsou.linop.base.PyLopLinearOperator

Examples

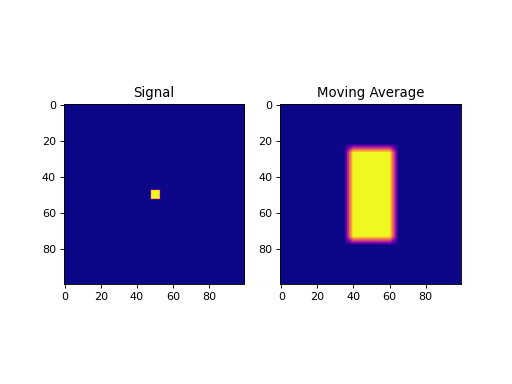
import numpy as np
import matplotlib.pyplot as plt
from pycsou.linop.conv import MovingAverage2D
from scipy import signal
sig = np.zeros(shape=(100,100))
sig[sig.shape[0] // 2 - 2:sig.shape[0] // 2 + 3, sig.shape[1] // 2 - 2:sig.shape[1] // 2 + 3] = 1
MAOp = MovingAverage2D(window_shape=(50,25), shape=sig.shape)
moving_average = (MAOp * sig.ravel()).reshape(sig.shape)
plt.figure()
plt.subplot(1,2,1)
plt.imshow(sig, cmap='plasma'); plt.title('Signal')
plt.subplot(1,2,2)
plt.imshow(moving_average, cmap='plasma'); plt.title('Moving Average')
plt.show()

(Source code, png, hires.png, pdf)

../../_images/pycsou-linop-conv-5.png

Notes

The MovingAverage2D operator is a special type of convolution operator that convolves a 2D array with a constant 2d filter of size \(n_{smooth, 1} \quad \times \quad n_{smooth, 2}\):

\[y[i,j] = \frac{1}{n_{smooth, 1} n_{smooth, 2}} \sum_{l=-(n_{smooth,1}-1)/2}^{(n_{smooth,1}-1)/2} \sum_{m=-(n_{smooth,2}-1)/2}^{(n_{smooth,2}-1)/2} x[l,m]\]

Note that since the filter is symmetrical, the MovingAverage2D operator is self-adjoint.